Twitter tips
From time to time I tweet about Angular, TypeScript, RxJS and more. Here are my 💡tweets.
💡#JavaScript: There are three different syntaxes for assigning a function to an object property. Two ways for a usual function and one using an arrow function.

💡#JavaScript: If you initialize object properties with variables having the same name you can just put the names in the object.

💡In #TypeScript you can use Omit to create a type by removing properties of an existing type.

💡#TypeScript: I used to use the ternary operator when calling a function on an optional property, but now I prefer optional chaining combined with nullish coalescing. Find it more appropriate and readable.

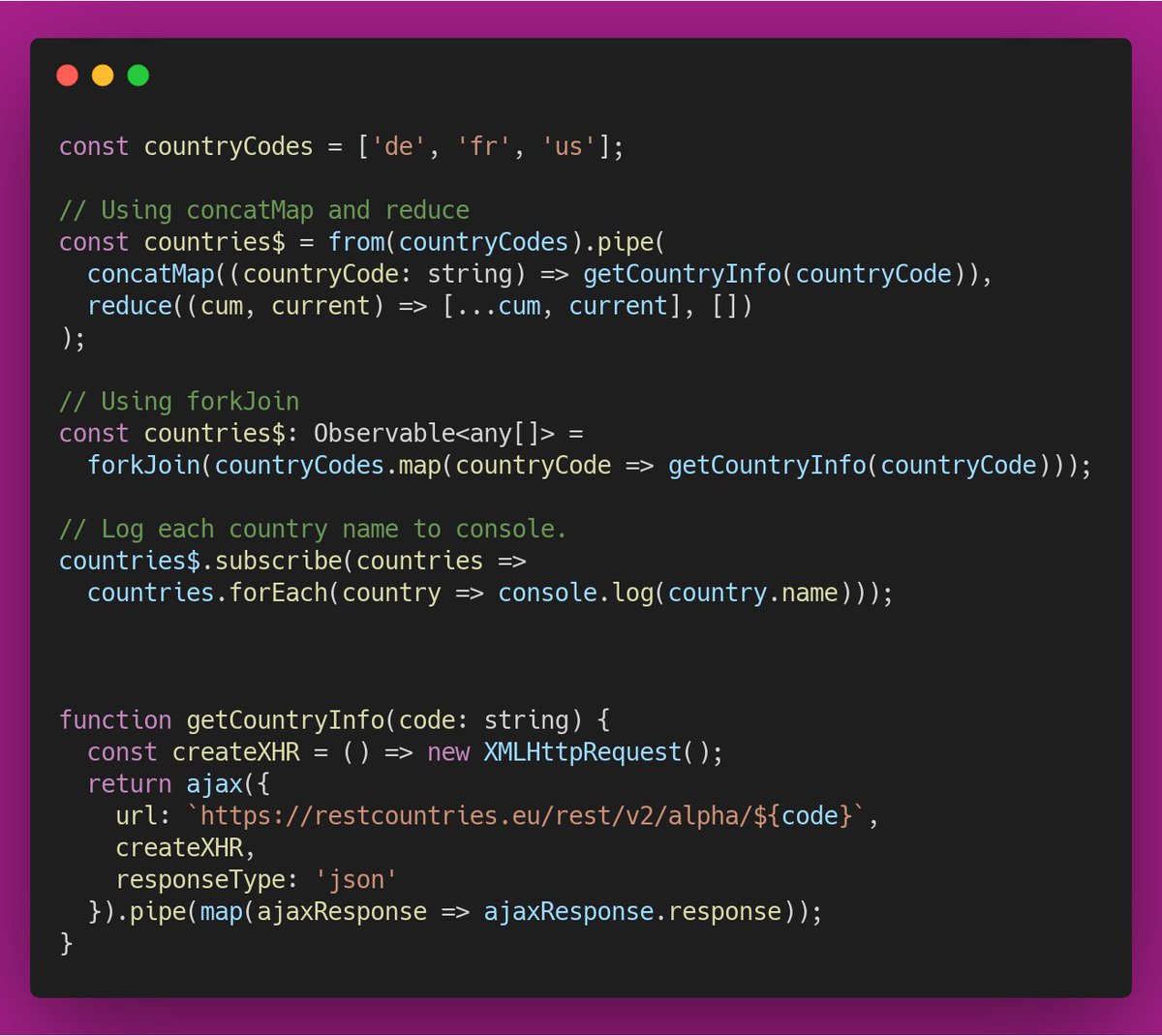
💡#RxJS: I used to merge several observables that emit one value each to an array of values by using the operators concatMap and reduce, but there is a much easier operator for this: forkJoin. forkJoin emits the last value of each observable and completes.
💡 I always try to avoid using the as operator in #TypeScript , since it is a cast and it bypasses static type checking.

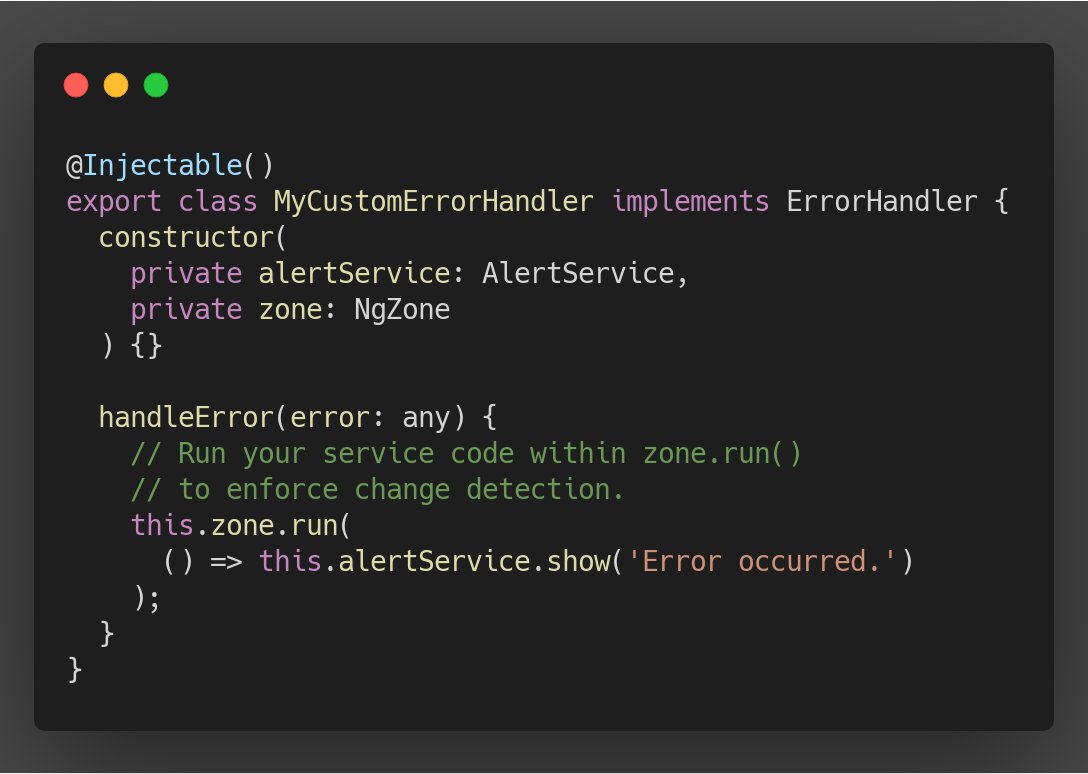
💡#Angular: I implemented a custom error handler that calls a service function to show an alert to the user. I noticed that there is no change detection run after handleError() was called. To fix this, the service function call must be wrapped in NgZone.run().
💡#Angular #RxJS: If you want to get values from an observable stream only when the value changes, e.g. if a specific query parameter changes, you can use distinctUntilChanged.

💡#RxJS: The tap operator has the same signature as the subscribe function, i.e. it takes up to three functions in its parameters, namely next(), error() and complete(). *BUT*: Implementing subscribe's error handler does not rethrow the error, tap's error handler does!

💡#TypeScript: If you want to use an existing interface, but the properties should be optional in your case, Partial can help you construct your object.

💡TIL: Add required inputs of an #Angular component to the component's selector string. The compiler will throw an error when the input attribute is missing.

💡#Angular: Having multiple subscribers to an HttpClient.get() fires multiple http requests. Sharing the result with #RxJS' shareReplay() leads to a single http request.

💡TIL: prefer ?? operator over || for default values in #typescript to avoid unintended behavior for 0, '' and NaN.

💡TIL: repo1.github.io and repo2.github.io are two different sites, because of this list: publicsuffix.org
💡TIL: #Angular‘s lifecycle hook ngOnDestroy is also available for services, not only for components.


